Kania Az Zahra (18) / XI IPS 2
1. lim x→0 x³ - 3x 2 + 6x / x² + 2x = ?
2. lim x→0 x / √1 + x - √1 - x = ?
3. lim x→3 √3 + x - √2x / 3 - x = ?
4. sebuah lempengan logam yang dipanaskan akan memuai dengan pertambahan luas sebagai fungsi waktu f(t) = 0,36t² + 0,6t² (cm²). kecepatan perubahan luas lempengan logam tersebut pada saat t menit dirumuskan dengan v = lim t→t₁ f(t) - f(t₁) / t-t₁. tentukan kecepatan perubahan luas lempengan logam pada saat t = 5 menit
5. sebuah mobil yang bergerak dengan kelajuan setiap saat dirumuskan dengan v(t) = 5t - ½ t², v dalam m/detik dan t dalam detik.
a. tentukan nilai pendekatan kelajuan untuk t mendekati 5
b. tentukan percepatan (dalam m/detik) pada saat t mendekati 3 detik percepatan = perubahan kelajuan/perubahan waktu = ⃤ v/ ⃤ t (m/det²)
1. tentukan turunan pertama dari: f(x) = (2x + 3)³
2. tentukan f'(x) dari: f(x) = 3x - 5/√4x - 10
3. turunan pertama dari f(x) =(2 - 6x)³ adalah f'(x) ?
4. tentukan gradien garis singgung kurva f(x) = x² + 3x - 4 di titik (2, 6)
5. gradien garis singgung kurva y = x³ - 2x di titik (1, -1)
6. persamaan garis singgung kurva y = 3x² - 5 di titik (-2, 7) adalah?
7. tentukan persamaan garis singgung pada kurva y = x³ + 10 di titik yang berordinat 18?
8. tentukan persamaan garis singgung pada kurva y = 12 - x⁴ - 7x² + 20 di titik yang berabsis 2?
9. garis yang menyinggung kurva y = 12 - x⁴ dan tegak lurus dengan x - 32y = 48 mempunyai persamaan?
10. gradien dengan garis singgung y = x² - 8x + 12 kurva di titik (1, 5) sama dengan?
1. lim x→2 2x + 3x² =
2. lim x→3 (x² - 5)³ =
3. lim x→5 (-3) =
4. nilai lim x→2 (x-4) =
5. nilai lim x→1 x² - 1/x - 1 =
6. diketahui fungsi f(x) sebagai berikut f(x) = {x 2 -1, untuk x < -2, -2x -1 untuk x >2, nilai lim x→2 f(x)
8. jika lim x→3 f(x) = 5 dan lim x→3 g(x) = 9, nilai lim x→3 f(x) + g(x)/2f(x) adalah?
9. diketahui lim x→α f(x) = p, nilai lim x→α (f(x) + 1² - 3f(x)) adalah?
10. lim x→-1 2x² - x - 3/3x² + 8x + 5 =
1. jika diketahui f(r) = 2r^1,5 - 2r^½, maka nilai f'(1) =
2. sebuah persegi dengan sisi x memiliki luas f(x). nilai f'(6) =
3. besar populasi di suatu daerah t tahun mendatang di tentukan oleh persamaan p(t) = 10³ t² - 5.10² t + 10⁶. laju pertumbuhan penduduk 5 tahun mendatang adalah?
4. dua bilangan bulat m dan n memenuhi hubungan 2m - n = 40. nilai minimum dari p = m² + n² adalah?
5. diberikan fungsi f(x) = ax² + bx + c jika f'(0) = 2, dan f(2) = 6, tentukan nilai a, b, dan c.









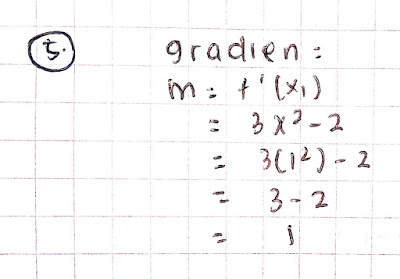




















No comments:
Post a Comment