CONTOH SOAL CERITA NILAI OPTIMUM

Nama: Kania Az Zahra

Kelas: XI IPS 2

1. Dewi akan membuat 2 model pakaian jadi. model I memerlukan tidak lebih dari 1m kain polos dan 1,5m kain bergaris. model II memerlukan tidak lebih dari 2m kain polos dan 0,5m kain bergaris. bila pakaian tersebut dijual, setiap model I memperoleh untung tidak kurang dari Rp 15.000 dan model II memperoleh untung tidak kurang dari Rp 10.000. laba yang diperoleh Dewi adalah sebanyak?

Ditanya:

buat pertidaksamaannya dulu baru table setelah itu daerah kotor dan daerah bersihnya, himpunan penyelesaian, titik pojok untuk menentukan nilai optimalnya dan laba dewi dari nilai tertinggi yang diperoleh

Pembahasan:

diketahui:

model kain I: kain polos 1m dan kain bergaris 1,5m 

model kain II: kain polos 2m dan kain bergaris 0,5m 

persediaan: 

- kain polos 20m

- kain bergaris 10m

laba:

- model I tak kurang dari Rp 15.000

- model II tak kurang dari Rp 10.000

ditanya: laba yang diperoleh

jawab:

model I = x

model II = y

 

	Kain polos	Kain bergaris
Model  1 (x)	1x	1,5x
Model 2 (y)	2y	0,5y
persediaan	20	10

 

persamaan:

1x + 2y = 20

1,5x + 0,5y = 10

 

penyelesaian menggunakan metode matematika yaitu eliminasi dan subtitusi

 

setelah persamaan diselesaikan, masukkan hasil persamaan kedalam rumus untuk mencari laba

jadi, laba yang diperoleh adalah: Rp 140.000

daerah bersih dan kotor: 

2. Ling ling membeli 240 ton beras untuk dijual lagi. Ia menyewa dua jenis truk untuk mengangkut beras tersebut. Truk jenis A memiliki kapasitas 6 ton dan truk jenis B memiliki kapasitas 4 ton. Sewa tiap truk jenis A adalah Rp 100.000,00 sekali jalan dan truk jenis B adalah Rp 50.000,00 sekali jalan. Maka Ling ling menyewa truk itu sekurang-kurangnya 48 buah. Berapa banyak jenis truk A dan B yang harus disewa agar biaya yang
dikeluarkan minimum?

 

kendala-kendalanya dapat dituliskan sebagai berikut. 

x + y ≥ 48,

6x + 4y ≥ 240,

x ≥ 0, y ≥ 0, x, y anggota bilangan cacah

Dengan fungsi objektifnya adalah f(x, y) = 100.000x + 50.000y.

Gambarkan daerah penyelesaian dari kendala-kendala di atas.  

Titik pojok dari daerah penyelesaian di atas adalah titik potong garis 6x + 4y = 240 dengan sumbu-y, titik potong garis x + y = 48 dengan sumbu-x, dan titik potong garis-garis x + y = 48 dan 6x + 4y = 240. Titik potong garis 6x + 4y = 240 dengan sumbu-y adalah titik (0, 60). Titik potong garis x + y = 48 dengan sumbu-x adalah titik (48, 0). Sedangkan titik potong garis-garis x + y = 48 dan 6x + 4y = 240 dapat dicari dengan menggunakan cara eliminasi

 

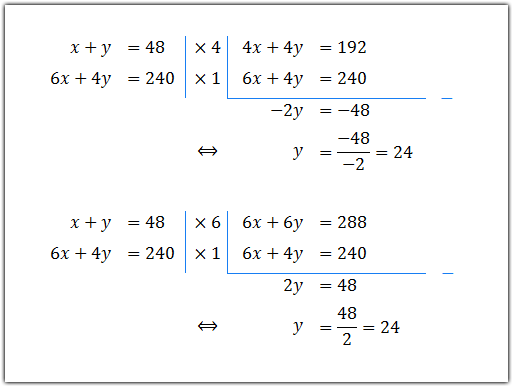
Diperoleh, titik potong garis-garis x + y = 48 dan 6x + 4y = 240 adalah pada titik (24, 24).

Substitusikan koordinat setiap titik pojok itu ke dalam fungsi objektif.

 Dari ketiga hasil tersebut, dapat diperoleh bahwa agar biaya yang dikeluarkan minimum, Ling ling harus menyewa 60 truk jenis B dan tidak menyewa truk jenis A.

 

3. Seorang tukang roti mempunyai bahan A,B dan C masing-masing sebanyak 160 kg, 110 kg dan 150 kg.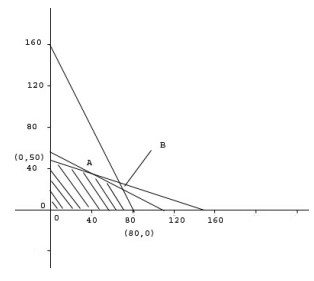

• Roti I memerlukan 2 kg bahan A, 1 kg bahan B dan 1 Kg bahan C
• Roti II memerlukan 1 kg bahan A, 2 kg bahan B dan 3 Kg bahan C

Sebuah roti I dijual dengan harga Rp.30.000 dan sebuah roti II dijual dengan harga Rp.50.000, pendapatan maksimum yang dpat diperoleh tukang roti tersebut adalah…

Misal roti I = x dan roti II = y didapat persamaan sbb:

• 2x + y ≤ 160 …..(1)
• x + 2y ≤ 110 …..(2)
• x + 3y ≤ 150 ….(3)

buat sketsa grafiknya:

Daerah yang diarsir adalah himpunan penyelesaian dari tiga grafik tsb. Didapat 4 titik ekstrim yaitu (0,50), (80,0), titik A dan titik B

perpotongan (1) dan (2)  → titik B

4. Untuk mengetahui pendapatan maksimum, maka terlebih dahulu kita menyusun sistem pertidaksamaan dan fungsi tujuan dari soal cerita tersebut. Karena yang ditanya pendapatan maksimum, maka tentu harga jual kue merupakan fungsi tujuan pada soal ini. Untuk menyusun sistem pertidaksamaan, yang perlu kita lakukan adalah menentukan variabel dan koefisiennya.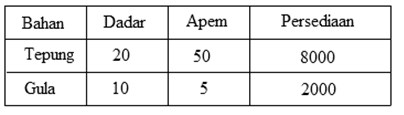

Bahan yang tersedia:

• Tepung = 8 kg = 8000 g
• Gula = 2 kg = 2000 g

Misalkan :

• kue dadar = x
• kue apem = y 

Maka jumlah tepung, gula, dan harga jual merupakan koefisien. Agar lebih mudah, kita dapat memasukkan data yang ada pada soal ke dalam bentuk tabel seperti berikut :

Dari tabel di atas dapat disusun sistem pertidaksamaan sebagai berikut :

20x + 50y = 800 → 2x + 5y ≤ 800

10x +5y = 2000 → 2x + y ≤ 400

x ≥ 0 dan y ≥ 0 

dengan fungsi tujuan f(x,y) = 300x + 500y 

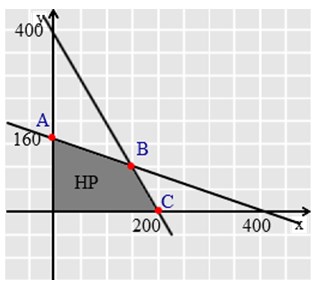
Kemudian gambarkan sistem pertidaksamaan yang sudah disusun dalam grafik.

Untuk garis 2x + 5y = 800

x = 0, y = 160 → (0, 160)

y = 0, x = 400 → (400, 0)

Untuk garis 2x + y = 400

x = 0, y = 400 → (0, 400)

y = 0, x = 200 → (200, 0)

Titik B merupakan titik potong garis 2x + 5y = 800 dengan garis 2x +

y = 400

2x + y = 400

y = 400 – 2x

Dengan metode substitusi :

2x + 5y = 800

2x + 5(400 – 2x) = 800

2x + 2000 – 10x = 800

-8x = -1200

x = 150

Karena x = 150, maka :

y = 400 – 2x

y = 400 – 2(150)

y = 400 – 300

y = 100

Dengan demikian titik B (150, 100)

Selanjutnya substitusikan titik A, B, dan C ke fungsi tujuan :

A(0, 160) → F(x,y) = 300(0) + 500(160) = 80.000

B(150, 100) → F(x,y) = 300(150) + 500(100) = 95.000

C(200, 0) → F(x,y) = 300(200) + 500(0) = 60.000

Jadi, pendapatan maksimum yang bisa diperoleh pedagang kue itu adalah Rp 95.000,00.

sumber:

• https://yos3prens.wordpress.com/2012/11/26/program-linear-menentukan-nilai-optimum-suatu-fungsi-objektif-dengan-menggunakan-metode-uji-titik-pojok/
• https://soalkimia.com/contoh-soal-program-linear/