Nama: Kania Az Zahra
Kelas: XI IPS 2
Pengertian Matriks
Matriks adalah susunan bilangan (elemen) yang disusun berdasarkan baris
dan kolom sehingga berbentuk persegi panjang. Baris dalam matriks
merupakan susunan dari bilangan-bilangan yang mendatar. Sedangkan kolom
dalam matriks merupakan susunan dari bilangan-bilangan yang tegak.
Ordo Matriks
banyaknya baris dan kolom dalam matriks disebut dengan ordo. Banyaknya
baris dan kolom dalam matriks akan menentukan ukuran dari matriks, hal
ini disebut dengan ordo matriks.
Macam-Macam Matriks
1. Matriks Baris dan Matriks Kolom
Matriks baris adalah suatu matriks yang hanya memiliki satu baris saja.
Sedangkan, matriks kolom adalah suatu matriks yang hanya memiliki satu
kolom saja. Contoh:
A = (1 4) atau B = (3 7 9) adalah matriks baris
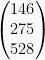 atau
atau  adalah matriks kolom
adalah matriks kolom
2. Matriks Persegi Matriks yang memiliki jumlah kolom dan baris yang sama disebut matriks persegi. Matriks persegi memiliki ordo n.
Contoh:
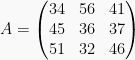 adalah matriks persegi berordo 3, atau
adalah matriks persegi berordo 3, atau
 adalah matriks persegi berordo 2.
adalah matriks persegi berordo 2.
3. Matriks Segitiga Atas dan Seigitiga Bawah
Matriks persegi A yang memiliki elemen matriks  untuk
untuk  atau elemen-elemen matriks dibawah diagonal utama bernilai 0 disebut
matriks segitiga atas. Matriks persegi A yang memiliki elemen matiks
atau elemen-elemen matriks dibawah diagonal utama bernilai 0 disebut
matriks segitiga atas. Matriks persegi A yang memiliki elemen matiks 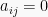 untuk
untuk 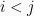 atau elemen-elemen matriks diatas diagonal utama bernilai 0 disebut matriks segitiga bawah.
atau elemen-elemen matriks diatas diagonal utama bernilai 0 disebut matriks segitiga bawah. Contoh:
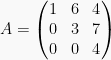 adalah matriks segitiga atas,
adalah matriks segitiga atas,
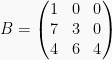 adalah matriks segitiga bawah.
adalah matriks segitiga bawah.
4. Matriks Diagonal
Matriks persegi A yang memiliki elemen matiks 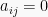 untuk
untuk  atau elemen-elemen matriks diluar diagonal utama bernilai 0 disebut matriks diagonal.
atau elemen-elemen matriks diluar diagonal utama bernilai 0 disebut matriks diagonal. Contoh:
 atau
atau 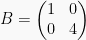
5. Matriks Skalar Matriks diagonal yang memiliki elemen-elemen pada diagonal utamanya bernilai sama disebut matriks skalar.
Contoh:
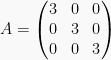 atau
atau 
6. Matriks Identitas Matriks identitas adalah matriks skalar yang bilangannya semua 1Contoh :
 atau
atau 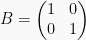
7. Matriks Simetris
Matriks persegi A yang memiliki elemen matiks baris ke-I sama dengan
elemen matriks kolom ke-j untuk i = j disebut simetris. Atau, dapat
dikatakan elemen 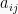 sama dengan elemen
sama dengan elemen 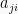 .
. Contoh:
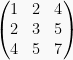
Dapat dilihat bahwa elemen baris ke-1 sama dengan kolom ke-1, baris
ke-2 sama dengan kolom ke-2, dan baris ke-3 sama dengan kolom ke-3.
8. Transpose Matriks
Transpose matriks merupakan perubahan baris menjadi kolom dan sebaliknya. Transpose matriks dari  adalah sebuah matriks dengan ukuran (n x m) dan bernotasi AT. Jika matriks A ditanspose, maka baris 1 menjadi kolom 1, baris 2 menjadi kolom 2, dan begitu seterusnya.
adalah sebuah matriks dengan ukuran (n x m) dan bernotasi AT. Jika matriks A ditanspose, maka baris 1 menjadi kolom 1, baris 2 menjadi kolom 2, dan begitu seterusnya. Contoh:
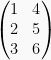 ditranspose menjadi
ditranspose menjadi  .
.
Sifat dari transpose matriks: 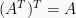 .
.
Operasi Matriks 1. Penjumlahan Matriks
Misalkan
terdapat dua buah matriks, yaitu matriks A dan matriks B. Jika matriks C
adalah matriks penjumlahan dari A dengan B, maka matriks C dapat diperoleh dengan menjumlahkan setiap elemen pada matriks A yang seletak dengan setiap elemen pada matriks B. Oleh karena itu, syarat agar dua atau lebih matriks dapat dijumlahkan adalah harus memiliki ordo yang sama.
Contoh:

Hasil dari A + B dapat diperoleh dengan menjumlahkan setiap elemen matriks A yang seposisi dengan setiap elemen matriks B.
 2. Pengurangan Matriks
2. Pengurangan Matriks Misalkan
terdapat dua buah matriks, yaitu matriks A dan matriks B. Jika matriks C
adalah matriks pengurangan dari A dengan B, maka matriks C dapat diperoleh dengan mengurangkan setiap elemen pada matriks A yang seletak dengan setiap elemen pada matriks B. A - B = A + (-B)
Contoh:

Hasil dari A - B dapat diperoleh dengan mengurangkan setiap elemen matriks A yang seposisi dengan setiap elemen matriks B.

3. Perkalian Matriks
Contoh:
Jadi, a11 akan dikalikan dengan b11, a12 dikalikan dengan b21, a21 dikalikan dengan b11, dan a22 dikalikan dengan b21.

Lalu, jumlahkan hasil kali elemen-elemennya menjadi seperti ini:

Sehingga, hasil kali matriks A dengan matriks B adalah sebagai berikut:

Sumber:https://www.studiobelajar.com/matriks-dasar/
https://blog.ruangguru.com/matematika-kelas-11-operasi-aljabar-pada-matriks-penjumlahan-pengurangan-dan-perkalian
atau
adalah matriks kolom
adalah matriks persegi berordo 3, atau
adalah matriks persegi berordo 2.
adalah matriks segitiga atas,
adalah matriks segitiga bawah.
atau
atau
ditranspose menjadi
.
.








No comments:
Post a Comment