Kania Az Zahra : SOAL PENYELESAIAN MENGGUNAKAN MATRIKS

Monday, September 7, 2020

SOAL PENYELESAIAN MENGGUNAKAN MATRIKS

Nama: Kania Az Zahra (17)

Kelas: XI IPS 2

Soal determinan matriks berordo 3x3 dan 2x2

Ordo 2x2

1. Hitunglah berapa nilai determinan dari matriks ordo 2 x 2 berikut ini :

Pembahasan:

2. Hitunglah berapa nilai determinan dari matriks ordo 2 x 2 berikut ini :

Pembahasan:

Ordo 3x3

1. Hitunglah berapa nilai determinan dari matriks ordo 3 x 3 berikut ini :

Pembahasan:

det( A ) = ( 2 . 4 . 1 ) + ( 3 . 3 . 7 ) + ( 4 . 5 . 0 ) – ( 4 . 4 . 7 ) – ( 2 . 3 . 0 ) – ( 3 . 5 . 1 )
= ( 8 ) + ( 63 ) + ( 0 ) – ( 112 ) – ( 0 ) – 15
= – 56

2. Hitunglah berapa nilai determinan dari matriks ordo 3 x 3 berikut ini :

Pembahasan:

det( A ) = ( 1 . 1 . 2 ) + ( 2 . 4 . 3 ) + ( 3 . 2 . 1 ) – ( 3 . 1 . 3 ) – ( 1 . 4 . 1 ) – ( 2 . 2 . 2 )
= ( 2 ) + ( 24 ) + ( 6 ) – ( 9 ) – ( 4 ) – ( 8 )
= 11

Jadi, nilai determinan dari matriks ordo 3 x 3 di atas ialah = 11.

Soal kofaktor matriks 2x2 dan 3x3

Ordo 2x2

Tentukanlah kofaktor dari matriks

$A=\begin{bmatrix}2&4\\3&5\end{bmatrix}$

Jawab :

Terlebih dulu kita cari minor dari matriks A tersebut. Disini minor dari matriks A di dapat :

$M_{A}=\begin{bmatrix}5&3\\4&2\end{bmatrix}$

Kemudian kita cari kofaktor tiap elemen dari minor tersebut :

Kofaktor Matriks A baris pertama kolom pertama, berarti i = 1 dan j = 1.

$K_{11}=(-1)^{i+j}. M_{ij}$

$K_{11}=(-1)^{1+1}. M_{11}$

$K_{11}=(-1)^{2}.5$

$K_{11}=1.5=5$

Kofaktor matriks A baris pertama kolom kedua, berarti i = 1 dan j = 2.

$K_{12}=(-1)^{1+2}.M_{12}$

$K_{12}=(-1)^{3}.M_{12}$

$K_{12}=(-1).3=-3$

Kofaktor matriks A baris kedua kolom pertama, berarti i = 2 dan j = 1

$K_{21}=(-1)^{2+1}.M_{21}$

$K_{21}=(-1)^{3}.4$

$K_{21}=-4$

Kofaktor matriks A baris kedua kolom kedua, berarti i = 2 dan j = 2

$K_{22}=(-1)^{2+2}.M_{22}$

$K_{22}=1.2=2$

Jadi, kofaktor dari matriks A adalah

$K_{A}=\begin{bmatrix}5&-3\\-4&2\end{bmatrix}$

Adjoin merupakan transfus dari kofaktor matriks A. secara matematis dirumuskan sebagai :

$Adj A=K_{A}^{T}$

Dimana :

$K_{A}^{T}$ = Transfus kofaktor dari matriks A

Adj A = adjoin matriks A

Dari soal di atas , maka kita bisa menentukan adjoinnya adalah sebagai berikut :

$Adj A =K_{A}^{T}$

$Adj A=\begin{bmatrix}5&-4\\-3&2\end{bmatrix}$

Ordo 3x3

Tentukanlah Kofaktor dan Adjoin dari matriks berikut :

$A=\begin{bmatrix}2&4&6\\1&3&2\\0&1&2\end{bmatrix}$

Penyelesaian :

Terlebih dahulu kita cari minor matriks A, disini didapat bahwa minor matriks A adalah :

$A=\begin{bmatrix}4&0&1\\2&4&2\\10&-2&2\end{bmatrix}$

Sehingga kofaktor matriks A adalah :

$A=\begin{bmatrix}4&0&1\\-2&4&-2\\10&2&2\end{bmatrix}$

Adjoin matriks A dicari dengan mencari transfus dari kofaktor matriks A, sehingga :

$Adj A=\begin{bmatrix}4&2&10\\0&4&-2\\1&2&2\end{bmatrix}$

Invers matriks berordo 2x2 dan 3x3

Ordo 2x2

Menentukan matriks invers dari!

Jawaban :

Berikutnya, baris kedua dari kolom pertama dan baris pertama dari kolom kedua dikalikan dengan -1. Hasilnya adalah sebagai berikut.

jawaban soal invers matriks

Selanjutnya, cari determinan matriks
det = (2 × 6) – (4 × 1)
= 12 – 4
= 8

Setelah nilai adjoin dan determinan matriks diketahui. Kemudian masukkan rumus matriks di atas. Hasilnya adalah :

jawaban invers matriks

Ordo 3x3

Matriks A dikenal sebagai berikut : contoh soal matriks 3x3

Jawaban :

jawaban matriks 3x3

Sumber:

https://rumus.co.id/determinan-matriks/

https://rumusrumus.com/invers-matriks

https://ilmuhitung.com/menentukan-kofaktor-dan-adjoin-suatu-matriks/

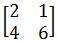
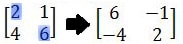
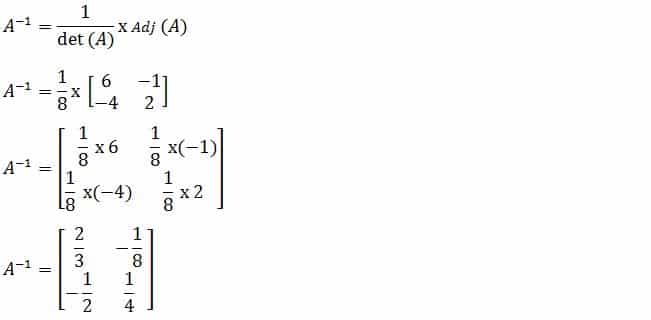
No comments:

Post a Comment

Subscribe to: Post Comments (Atom)