Nama: Kania Az Zahra (18)
Kelas: XI IPS 2
Barisan merupakan urutan dari suatu anggota-anggota himpunan berdasarkan
suatu aturan tertentu. Setiap anggota himpunan diurutkan pada
urutan/suku pertama, kedua, dan seterusnya. Untuk menyatakan urutan/suku
ke-n dari suatu barisan dinotasikan 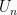 .
Barisan juga dapat didefinisikan sebagai fungsi dari bilangan asli atau
fungsi yang domainnya himpunan bilangan asli. Sehingga,
.
Barisan juga dapat didefinisikan sebagai fungsi dari bilangan asli atau
fungsi yang domainnya himpunan bilangan asli. Sehingga, 
Misalkan 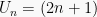 , maka suku ke-4 dari baris tersebut adalah
, maka suku ke-4 dari baris tersebut adalah  .
.
Penjumlahan suku-suku dari suatu barisan disebut deret. Penjumlahan
suku-suku tersebut bisa dibuat dalam bentuk sigma. Barisan dari suku U1, U2, U3, …, Un yang dinyatakan dalam fungsi f(n) = Un memiliki deret sebagai:
Baris Aritmatika
Baris aritmatika merupakan baris yang nilai setiap
sukunya didapatkan dari suku sebelumnya melalui penjumlahan atau
pengurangan dengan suatu bilangan b. Selisih antara nilai suku-suku yang
berdekatan selalu sama yaitu b. Sehingga:
Sebagai contoh baris 1, 3, 5, 7, 9, merupakan baris aritmatika dengan nilai:
b = (9 – 7) = (7 – 5) = (5 – 3) = (3 – 1) = 2
Untuk mengetahui nilai suku ke-n dari suatu barisan aritmatika dapat
diketahui dengan mengetahui nilai suku ke-k dan selisih antar suku yang
berdekatan (b). rumusannya berikut ini:
Jika yang diketahui adalah nilai suku pertama 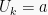 dan selisih antar sukunya (b), maka nilai k = 1 dan nilai
dan selisih antar sukunya (b), maka nilai k = 1 dan nilai 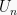 adalah:
adalah:
Deret Aritmatika
Deret aritmatika adalah penjumlahan suku-suku dari
suatu barisan aritmatika. Penjumlahan dari suku-suku petama sampai suku
ke-n barisan aritmatika dapat dihitung sebagai:
atau sebagai:
Jika hanya diketahui nilai a dalalah suku pertama dan nilai adalah suku ke-n, maka nilai deret aritmatikanya adalah:
Persamaan tersebut bisa dibalik untuk mencari nilai suku ke-n menjadi:
Sehingga diperoleh  .
.
Sisipan
Jika hendak membuat sebuah baris aritmatika dengan telah diketahui
nilai suku pertama (a) dan suku terakhirnya (p), dapat disisipkan
sejumlah bilangan diantara keduan bilangan tersebut. Sejumlah bilangan
(q buah) tersebut menjadi suku-suku baris aritmatika dan memiliki
selisih antar suku beredekatan (b). Baris aritmatika tersebut memiliki
jumah suku q + 2 dan diurut berupa:
a, (a + b), (a + 2b), (a + 3b), …, (a + q.b), (a + (q+1)b)
Diketahui bahwa suku terakhir:
(a + (q+1)b) = p
Maka, nilai b dapat ditentukan sebagai:
Misalkan a= 1 dan p = 9, jika disisipkan 3 bilangan diantara a dan p, maka baris belangan aritmatikanya adalah:
- Nilai q = 3
- Jumlah suku = q + 2 = 3 + 2 = 5
- Baris aritmatika : 1, 3, 5, 7, 9
Suku Tengah
Jika barisan aritmatika memiliki jumlah suku ganjil, maka memiliki suku tengah. Suku tengah baris aritmatika adalah suku ke-  . Jika diselesaikan dalam rumus
. Jika diselesaikan dalam rumus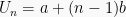 , maka nilai suku tengah didapatkan:
, maka nilai suku tengah didapatkan:
Contoh soal
1. Jumlah suku yang pertama dari barisan 20 + 15 + 10 +…… adalah …..
a). -550
b). -250
c). -75
d). -115
e). -250
Penyelesaian :
a = 20
b = U2-U
= 15-
= -5
Sn = n (a + Un)Un = a + (n – 1) bU20 = 20 + (20-1)(-5)= 20 + (19) (-5)= 20 – 95= – 75S20 = 20 (20 + (-75))= 10 (-55)S20 = – 550
Jawaban: a
2. Jumlah 10 suku pertama dari deret aritmatika : 3 + 5 + 7 + 9 + ….. adalah?
a). 105
b). 120
c). 150
d). 155
e). 1
penyelesaian
a = 3
b = U3 – U2 – 1
= U3 – U2
= 7 – 5
= 2
Sn = n (2a + (n-1)b)= 10 (2 (5) + (10-1)2)= 5 (6+9) 2= 120
Jawaban: b
3. Diketahui barisan aritmatikan dengan U4 = 11 dan U8 = 23. Suku ke 15 dari suku barisan aritmatika itu
a). 345
b). 44
c). 49
d). -40
e). -44
Penyelesaian :
Un = a + (n-1)b= a + (4-1)b = 11= a + 36 = 11U8 = a + (8-1)b = 23= a + 7b = 23
Eliminasi a + 3b = 11
a + 7b = 23
-4b = -12
b = = 3
Substitusi a + 3b = 11
a + 3 (3) = 11
a + 9 = 11
a = 11 – 9 = 2
Jawaban: bU15Un = a + (n-1) bU15 = 2 + (15-1) 3= 2 + (14 x 3) = 44
4. Dari suatu barisan aritmatika diketahui U2 = 7 dan U6 = 19. Suku ke 8 dari barisan aritmatika tersebut adalah …..
a). 25
b). 26
c). 28
d). 31
e). 34
Penyelesaian :
Un = a + (n-1) bU2 = a + (2-1) b = 7= a + 1b = 7U6 = a + (6-1)b = 19= a + 5b = 19
Eliminasi :
a + 1 b = 7a + 5b = 19-4b = -12b = – = 3
Subtitusi :
b = 3a + 1 b = 7a + 1 (3) = 7a + 3 = 7a = 7 -3 = 4U8Un = a + (n-1) bU8 = 4 + (8-1) 3= 4 + (7 . 3)= 25
Jawaban: a
5. Dari suatu barisan aritmatika diketahui U10 = 41 dan U5 = 21. U20 barisan tersebut adalah …..
a). 69
b). 73
c). 77
d). 81
e). 83
Penyelesaian :
Un = a + (n-1) bU10 = a + (10-1)b = 41U5 = a + (5-1)b = 21a + 4b = 21
eliminasi :
a + 9b = 41a + 4b = 215b = 20b = = 4
subtitusi :
b = 4a + 9b = 415 +a + (9.4) = 41a + 36 = 41a = 41- 36= 5U20Un = a + (n-1)bU20 = a + (n-1) bU20 = 5 + (20+1) 4= 5 + (19.4)= 5 + 76= 81
Jawaban: d
Sumber
No comments:
Post a Comment