Nama: Kania Az Zahra (18)
Kelas: XI IPS 2
2.
3. 
4. 
5.
6. 
7. n_ > 5 = {1, 2, 3, 4, 5}
2n - 3 < 2n - 2
= 2(1) - 3 < 2(1) - 2
= (-1) < 0 (benar)
2(2) - 3 < 2(2) - 2
= 1 < 2 (benar)
2(3) - 3 < 2(3) - 2
=3 < 4 (benar)
2(4) -3<2(4) -2
= 5 < 6 (benar)
2(5) -3<2(5) -2
=7<8( benar)
8. 
Diketahui:
5kg gula + 30kg beras = 410.000
2kg gula + 60kg beras = 740.000
Ditanya : 2kg gula + 5kg beras ?
Jawab:
gula = x
beras = y
5x + 30y = 410.000 |*2
2x + 60y = 740.000 |*1
10x + 60y = 820.000
2x + 60y = 740.000
_______-
8x = 80.000
x = 10.000
subtitusikan x nya ke persamaan
2x + 60y = 740.000
2(10.000) + 60y = 740.000
20.000 + 60y = 740.000
60y = 720.000
y = 12.000
jadi, harga 1kg gula = Rp 10.000 dan 1kg beras = Rp 12.000
maka 2kg gula dan 5kg beras
= 2(10.000) + 5(12.000)
= 20.000 + 60.000
= Rp 80.000
10. tentukan daerah bersih dari pertidaksamaan linear berikut 5x + 3y ≤ 15
jawaban :
5x + 3y ≤ 15 uji 0
x = 0 | x = 0 5(0) + 3(0) ≤ 15
y = 5 | y = 3 0 ≤ 15 (benar)
11. 2x - 5y > 20
Cara penyelesaian :
a. Mencari x dan y
x 0 10
y -4 0
b. Menentukan dan letak daerah kotor
2(0) - 5(0) > 20
0 > 20 (salah)
c. Membuat garis koordinat
5x + 6y ≥ 30 (0,5) (6,0) *karena a positif dan tanda ≥ maka daerahnya berada di kanan garis
2x + y ≤ 0 (0,0) (0,0) *karena a negatif dan tanda ≤ maka daerahnya berada di kanan garis
Y ≥ 2 *daerah berada pada rentang y ≥ 2, y € r
Maka daerah penyelesaian dari model mtk tsb berada di daerah III
13.
Daerah yang diarsir pada gambar adalah himpunan penyelesaian dari
sistem pertidaksamaan 3x + 5y ≤ 30 ; 2x - y ≤ 4 ; x ≥ 0 dan y ≥ 0.
Penyelesaian Soal :
LANGKAH PERTAMA (I)
Buatlah sistem pertidaksamaan pada setiap garis dengan menggunakan cara sebagai berikut :
Persamaan garis I melalui titik (0,6) dan (10,0) sehingga :
ax + by = ab
6x + 10y = 6.10
6x + 10y = 60 .... (÷2)
3x + 5y = 30
Kemudian
perhatikan daerah arsiran yang mengarah ke bawah atau melalui titik
(0,0). Jika arsiran melalui titik (0,0) maka jika diuji titik (0,0)
pernyataan dikatakan benar :
3x + 5y = 30
3.0 + 5.0 = 30
0 + 0 = 30
0 ≤ 30 (Benar)
Pertidaksamaannya : 3x + 5y ≤ 30
Persamaan garis II melalui titik (0,-4) dan (2,0) sehingga :
ax + by = ab
-4x + 2y = (-4).2
-4x + 2y = -8 .... (÷ 2)
-2x + y = -4
Kemudian
perhatikan daerah arsiran yang mengarah ke sisi kiri atau melalui titik
(0,0). Jika arsiran melalui titik (0,0) maka jika diuji titik (0,0)
pernyataan dikatakan benar :
-2x + y = -4
(-2).0 + 0 = -4
0 + 0 = -4
0 ≥ -4 (Benar)
Pertidaksamaannya :
-2x + y ≥ -4 .... (× -1)
2x - y ≤ 4
Kemudian pada arsiran juga terdapat garis x ≥ 0 dan y ≥ 0.
Sehingga pertidaksamaannya adalah :
3x + 5y ≤ 30 ; 2x - y ≤ 4 ; x ≥ 0 dan y ≥ 0.
14. Nilai Maksimum 3x + 2y ?
x + y > 5
sumbu x ; y = 0 ( 5, 0)
sumbu y ; x = 0 ( 0, 5)
maka Nilai Maksimumnya adalah
3x + 2y
(5,0) = 3(5) + 2(0) = 15
(0,5) = 3(0) + 2(5) = 10
Nilai maksimum nya adalah 15
15.
Diketahui:
X = banyaknya sedan
Y = banyaknya truk
Luas Parkiran:
Sedan= 15
Truk = 15
Kapasitas 420
Kuantitas:
Sedan = 1
Truk = 1
Kapasitas 60
Jawab:
• Persamaan garis 1 : 5x + 15y = 4200
Titik (0,0) merupakan salah satu himpunan penyelesaian dari
pertidaksamaan tersebut sehingga diperoleh
5x + 15y = 4200 disederhanakan menjadi
5x + 15y ≤ 4200
• Persamaan garis 2 : x + y = 60
Titik (0,0) merupakan salah satu himpunan penyelesaian dari
pertidaksamaan tersebut sehingga diperoleh
x + y = 60 disederhanakan menjadi
x + y ≤ 60
• Kendala non negative diberikan oleh
x ≥ 0, y ≥ 0
• Jadi model matematika nya
5x + 15y ≤ 4200; 4x + y ≤ 60 ; x ≥ 0, y ≥ 0
Jawaban: 5x + 15y ≤ 4200; 4x + y ≤ 60 ; x ≥ 0, y ≥ 0
16.
Diketahui:
- Model I memerlukan 1 m kain polos dan 3 m kain bergaris.
- Model II memerlukan 2 m kain polos dan 1 m kain bergaris.
- Persediaan kain polos 20 m
- persediaan kain bergaris 20 m
- Harga jual model I Rp.150.000,00
- Harga jual model II Rp.100.000,00
Ditanya: Penghasilan maksimum yang dapat diperoleh = ...
Jawab :
(1) Kita Buat Tabel Untuk memudahkan:
Model || Polos || Garis || Harga
I || 1 || 3 || 150.000
II || 2 || 1 || 100.000
Stok || 20 || 20 || maksimum
(2) Kita buat kalimat matematika dari Tabel diatas Dengan kain polos sebagai (x) dan kain bergaris sebagai (y) :
x + 2y ≤ 20
3x + y ≤ 20
dengan :
x ≥ 0
y ≥ 0
Dan Fungsi Tujuan adalah harga jual :
150.000x + 100.000y
(3) Tentukan nilai fungsi x dan y pada grafik fungsi :
Dari x + 2y = 20 :
x = 0, y ⇒ 0 + 2y = 20
⇒ 2y = 20
⇒ y = 20/2
⇒ y = 10
Titik Koordinat ⇒ (0,10)
y = 0, x ⇒ x + 2y = 20
⇒ x + 0 = 20
⇒ x = 20
Titik Koordinat ⇒(20,0)
Dari 3x + y = 20
x = 0 , y ⇒ 3x + y = 20
⇒ 0 + y = 20
Titik Koordinat ⇒ (0,20)
y = 0, x ⇒ 3x + y = 20
⇒ 3x + 0 = 20
⇒ 3x = 20
⇒ x = 20/3
Titik Koordinat ⇒ (20/3,0)
Dari Titik - titik tersebut tarik garis lurus hingga terhubung.
Lalu kita cari titik potong dari garis tersebut, dengan metode eliminasi dan subtitusi :
Eliminasi y :
x + 2y = 20 | x 1 | x + 2y = 20
3x + y = 20 | x 2 | 6x + 2y = 40
============ -
-5x = -20
x = 20/5
x = 4
Subtitusikan nilai x pada persamaan 3x + y = 20 :
3 . 4 + y = 20
12 + y = 20
y = 20 - 12
y = 8
Koordinat titik potong garis pada (4,8)
(4) Selanjutnya Dari Titik - titik yang berpotongan kita uji dengan :
Fungsi Tujuan f(x,y) = 150.000x + 100.000y :
Ada 3 titik pada Grafik (perhatikan lampiran)
A. Titik (0,10) = 150.000 . (0) + 100.000 . (10) =
= 0 + 1.000.000 = 1.000.000
B. Titik (4,8) = 150.000 . (4) + 100.000 . (8) =
= 600.000 + 800.000 = 1.400.000
C. Titik (20/3,0) = 150.000 . (20/3) + 100.000 . (0) =
= 1.000.000 + 0 = 1.000.000
Dari Hasil Uji diatas dapat dilihat, penghasilan terbesar pada titik (4,8) yaitu sebesar Rp.1.400.000,00
17.
18.
Det(AtB) = (10.34) – (12.12) = 340 – 144 = 196
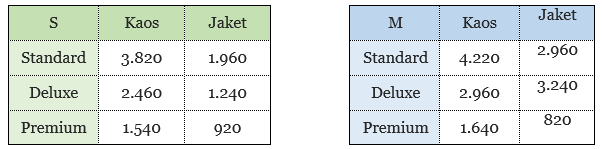
Sehingga, kita mendapatkan matriks-matriks produksi S dan M sebagai berikut.
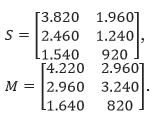
5x + 3y = 11.500 | x2 | 10x + 6y = 23000
4x + 2y = 9000 | x3 | 12x + 6y = 27000
——————-—-
-2x = -4000
x = 2000
5x + 3y = 11500
5(2000) + 3y = 11500
10000+ 3y = 11500
3y = 1500
y = 500
6(2000) + 5(500)
12000 + 2500
=14.500
Matriks A =
Matriks harga makanan adalah,
Matriks B =
⇔ AB = pemasukan harian Bu Ani
⇔ AB =
⇔ =%2B(10x3.000)%2B(5x1.000)%5C%5C(20x2.000)%2B(15x3.000)%2B(8x1.000)%5C%5C(15x2.000)%2B(20x3.000)%2B(10x1.000)%5Cend%7Barray%7D%5Cright%5D)
⇔ =
⇔ =
Jadi, pemasukan harian yang diterima Bu Ani dari setiap kantin A, kantin B, dan kantin C berturut-turut adalah Rp 55.000,00; Rp 93.000,00; dan Rp 100.000,00.
Total pemasukan harian Bu Ani dari seluruh kantin adalah Rp 55.000,00 + Rp 93.000,00 + Rp 100.000,00 = Rp 248.000,00
Jika ditulis dalam bentuk matriks:
-1(55)%5C%5C-3(16)%2B55%5Cend%7Barray%7D%5Cright%5D)
Jadi, Lisa bekerja selama 9 jam sedangkan Muri bekerja selama 7 jam.
Matriks rotasi 90° berlawanan jarum jam di pusat (0,0) adalah:
Menghasilkan komposisi transformasi:
x' = x + 1 = 3 + 1 = 4
y' = y + (-2) = -2 + (-2) = -4
Bayangan A = A' = (4,-4)
lanjut rotasi [O , 90°]
x" = -y' = -(-4) = 4
y" = x' = 4
Bayangan akhir = A" = (4,4)
19.
Diketahui
A =
Matriks A tidak mempunyai invers
Ditanyakan
x = .... ?
Jawab
Suatu matriks tidak mempunyai invers jika determinan matriks tersebut sama dengan nol
|A| = 0
(2x + 1)(5) – 3(6x – 1) = 0
10x + 5 – 18x + 3 = 0
8 – 8x = 0
8 = 8x
x = 
x = 1
20.
21.
22.
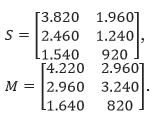
Untuk menentukan banyaknya total pakaian yang diproduksi oleh JCloth, kita jumlahkan matriks S’ dengan M’ seperti berikut.
Dari penjumlahan matriks di atas, kita memperoleh informasi banyaknya pakaian yang akan diproduksi oleh JCloth. Dengan menjumlahkan semua elemen-elemen matriks penjumlahan tersebut, kita peroleh bahwa banyaknya pakaian yang akan diproduksi oleh JCloth kurang lebih 28.142.
23. pensil (x) dan penghapus (y)
Maka:5x + 3y = 11.500 | x2 | 10x + 6y = 23000
4x + 2y = 9000 | x3 | 12x + 6y = 27000
——————-—-
-2x = -4000
x = 2000
5x + 3y = 11500
5(2000) + 3y = 11500
10000+ 3y = 11500
3y = 1500
y = 500
6(2000) + 5(500)
12000 + 2500
=14.500
24. Banyaknya makanan yang disetorkan setiap harinya adalah,
Matriks A =
Matriks harga makanan adalah,
Matriks B =
⇔ AB = pemasukan harian Bu Ani
⇔ AB =
⇔ =
⇔ =
⇔ =
Jadi, pemasukan harian yang diterima Bu Ani dari setiap kantin A, kantin B, dan kantin C berturut-turut adalah Rp 55.000,00; Rp 93.000,00; dan Rp 100.000,00.
Total pemasukan harian Bu Ani dari seluruh kantin adalah Rp 55.000,00 + Rp 93.000,00 + Rp 100.000,00 = Rp 248.000,00
25.
x + y = 16
3x + 4y = 55Jika ditulis dalam bentuk matriks:
Jadi, Lisa bekerja selama 9 jam sedangkan Muri bekerja selama 7 jam.
26. Transformasi geometri ↓
Pencerminan terhadap sumbu xA(a, b) → sb x → A'(a, -b)
Pencerminan terhadap sumbu y
A(a, b) → sb y → A'(-a, b)
Pencerminan terhadap garis y = x
A(a, b) → gr y = x → A'(b, a)
Pencerminan terhadap garis y = -x
A(a, b) → gr y = -x → A'(-b, -a)
Pencermianan terhadap titik pangkal koordinat
A(a, b) → titik pangkal → A'(-a, -b)
Pencerminan terhadap garis x = h
A(a, b) → garis x = h → A' (2h - a, b)
Pencerminan terhadap garis y = k
A(a, b) → garis y = k → A'(a, 2k - b)
Penyelesaian Soal
Bayangan titik A (-1, 4) oleh refleksi terhadap garis y= -x
Pencerminan terhadap garis y = -x
A(a, b) → gr y = -x → A'(-b, -a)
A(-1, 4) → gr y = -x → A'(-4, -(-1)) = (-4, 1)
27. (x, y) dicerminkan thp sumbu x : (x, -y) kemudian
(x, -y) dicerminkan thp sumbu y : (-x, -y)
Jadi
-x = x' => x = -x'
-y = y' => y = -y'
-y = y' => y = -y'
Bayangan dari : y = 3x² + 2x - 1 adalah
(-y') = 3(-x')² + 2(-x') - 1
-y' = 3x'² - 2x' - 1
y = -3x² + 2x + 1
(-y') = 3(-x')² + 2(-x') - 1
-y' = 3x'² - 2x' - 1
y = -3x² + 2x + 1
28. Matriks refleksi y = x adalah:
Matriks rotasi 90° berlawanan jarum jam di pusat (0,0) adalah:
Menghasilkan komposisi transformasi:
Memberikan:
Yang mana:
x = -x'
y = y'
Substitusi ke persamaan yang akan menghasilkan:
%2B5(y)-2%26%3D0%20%5C%5C%20-3x%2B5y-2%26%3D0%20%5C%5C%203x-5y%2B2%26%3D0%5Cend%7Balign%7D)
Yang mana:
x = -x'
y = y'
Substitusi ke persamaan yang akan menghasilkan:
Step-1 pencerminan garis x = k
Untuk x = 2
(x' , y') = (2(2) - x, y)
(x' , y') = (4 - x, y) akan disubtitusi ke Step-2
Step-2 translasi (- 3, 4)
Translasi (a, b) dengan a = -3 dan b = 4.
(x", y") = (x' + (- 3), y' + 4)
(x", y") = (4 - x + (- 3), y + 4)
(x", y") = (1 - x, y + 4)
Sehingga, x" = 1 - x dan y" = y + 4
Setelah diatur dengan pindah ruas menjadi
Substitusikan ke bentuk awal x²+ y² = 4
⇔ (1 - x")² + (y" - 4)² = 4
Selanjutnya tanda aksen dapat dihilangkan
⇔ (1 - x)² + (y - 4)² = 4
⇔ x² - 2x + 1 + y² - 8y + 16 = 4
⇔ x² + y² - 2x - 8y + 1 + 16 - 4 = 0
Dari langkah-langkah pengerjaan di atas, diperoleh persamaan bayangan lingkaran
30. A(3,-2)
dipetakan oleh T(1 -2)x' = x + 1 = 3 + 1 = 4
y' = y + (-2) = -2 + (-2) = -4
Bayangan A = A' = (4,-4)
lanjut rotasi [O , 90°]
x" = -y' = -(-4) = 4
y" = x' = 4
Bayangan akhir = A" = (4,4)
31. 
32.
refleksi terhadap sumbu x
x' = x
y' = -y
Bayangan
y = x² + 3x + 3
-y' = x'² + 3x' + 3
y = -x² - 3x - 3
• lanjut dilatasi [O, 4]
x' = 4x → x = 1/4 x'
y' = 4y → y = 1/4 y'
Bayangan akhir
y = -x² - 3x - 3
1/4 y' = -(1/4 x')² - 3(1/4 x') - 3
1/4 y = -1/16 x² - 3/4 x - 3
Kedua ruas kalikan 4
y = -1/4 x² - 3x - 12 ✔
33.
34. 
35. 
36. maka
U1,U2,U3,...
50.000, 55.000, 60.000,....
maka
a = 50.000
b = 5.000 (beda per bulan)
yang ditanyakan = jumlah tabungan dalam 2 tahun, maka jumlah tabungan dalam 24 bulan
maka
Sn = n/2 (a+Un)
cari Un dulu
Un = a + (n-1) b
U24 = 50.000 + (24-1) 5.000
U24 = 50.000 + 23 x 5.000
U24 = 50.000 + 115.000
U24 = 165.000
lalu
Sn = n/2 (a+Un)
S24 = 24/2 (50.000+165.000)
S24 =12 (215.000)
S24 = 2.580.000
U1,U2,U3,...
50.000, 55.000, 60.000,....
maka
a = 50.000
b = 5.000 (beda per bulan)
yang ditanyakan = jumlah tabungan dalam 2 tahun, maka jumlah tabungan dalam 24 bulan
maka
Sn = n/2 (a+Un)
cari Un dulu
Un = a + (n-1) b
U24 = 50.000 + (24-1) 5.000
U24 = 50.000 + 23 x 5.000
U24 = 50.000 + 115.000
U24 = 165.000
lalu
Sn = n/2 (a+Un)
S24 = 24/2 (50.000+165.000)
S24 =12 (215.000)
S24 = 2.580.000
37. 
38. 
39. 
40. 
